時間に対してサンプリングされたデータや空間データをフーリエ変換(FFT)することでスペクトルを求めて、それを用いて解析することは良く行われます。異常検知や正常異常判定においてもスペクトルに変換してそれを用いて判断することは一種の特徴量抽出と言えます。
多くの場合に用いられますのはFFT処理して得られる所謂スペクトルです。これは、FFTアナライザや最近ではディジタルオシロスコープでも得ることができて、異常検知の場合ですと正常な場合と異常な場合の特定の周波数帯のスペクトルの大きさの違いで判断されることが多いのです。例えば、FFTアナライザでは指定した周波数範囲のスペクトルの大きさが変化すると警告を出してくれます。
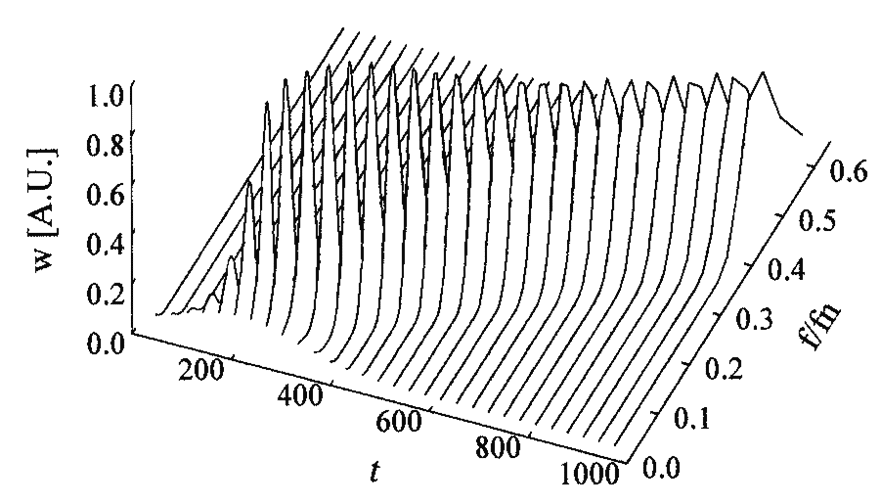
しかし、スペクトルはデータ区間で時間平均された結果なので周波数のみの関数となって時間の情報を持っておりません。したがって、時間に対して変化しない定常な信号(データ)の場合は問題ないのですが、時間に対して変化する非定常信号(データ)の場合には問題が起こります。そのような場合にはスペクトルが時間変化するので、その時間変化の様子に情報が含まれることが多いからです。その上、実際の現場で解析の対象となる信号の大部分は非定常信号です。
その様な非定常な信号の時間変化するスペクトルを求めてそれを使って解析・判断させるには非定常スペクトル解析法を用いる必要があります。非定常スペクトル解析法として最も有名なのが短時間フーリエ変換(Short Time Fourier Transform : STFT) で、それで求められた時間変化するスペクトルのことをスペクトログラムと言います。スペクトログラムの周波数分解能と時間分解能にはトレードオフの関係があり、両者を同時に高めることができませんのでデータに合わせて最適化することが重要です。さらに非定常スペクトル解析法としては、他にもより高い時間・周波数分解能が得られる「ウェーブレット変換」や「ウィグナー分布」と呼ばれる手法もあります。特に「ウェーブレット変換」は比較的欠点が少なく、変動が激しいデータに対しては「短時間フーリエ変換」よりも良い結果が得られる場合が多いので、最近は良く用いられるようになってきました。
「AI技研」は計測と計測データ処理及び非定常スペクトル解析法に関しても長年の実際的経験を有しておりますので、それらを最適化したり有効に活用したりすることについても多くの技術があります。